Very Near The Infallible Roulette Method
GEORGE RAYMON
NOTE: I want to thank the authors of "THE COMPLETE BOOK OF THE CASINO GAMES" for the great help that has meant for me the explanations found in their book and those which I refer to these pages.
INTRODUCTION.
This book is directed to the player of roulette. To the player that knows already basically the operation of the game. To the player that has proven other methods without success. And lack to him two very important things, a book that explains to him that what happens really in roulette, and a method that gives him some high guarantees of success in the game.
All we have read some book that fills pages and more pages on the theories of the random and the probabilities calculation without a subsequent practical application, and also we have proven methods "miraculous" that though make to win money when the situation is favorable do not notify of the dangers of an unfavorable situation, neither explain how surpassing it. These situations are presented more often than what we think and wish.
Precisely by these reasons, I will not extend in theoretical explanations. I will limit me to explain some indispensable basic notions to understand on that base has been built the method and below we will put in practice its game mechanism on real game sequences.
THE FIGURES.
(developed according to an explanation from the book "THE COMPLETE BOOK OF THE CASINO GAMES").
What are the figures? For the simple combinations of the roulette, a number anyone can be PAR or ODD, LACK or PASSES, RED or BLACK. We will center on this last combination.
We have two columns to note the combination of each play. If the number is red we make an annotation in the cabin of the left and if it is black in the right cabin. Each play can have an alone annotation, or to the right or the left, and it is one of the two possible alternatives: RED or BLACK. It is said that the possible figures of 1 (of one play) are 2. In the second consecutive play, the possibilities are: RED - RED, RED - BLACK, BLACK - RED, BLACK - BLACK, and is said that the figures of 2 are 4. In 3 consecutive plays, the possibilities are 8 (fig. 1).
GRAPHIC 1

The possibility of the fact that is formed a figure of 3 (1 between 8) is the half of being formed as a figure of 2 (1 between 4) and the fourth part that a figure of 1 (1 between 2). Is the same as to say:
So that could be formed one figure of 2 those of 1 will have been able to form 2 times each one, and so that could be formed one figure of 3 those of 2 will have been able to form also 2 times, and thus successive. For so much, we can say that the figures of 1 are double that those of 2, the figures of 2 are double that those of 3, the figures of 3 are double that those of 4, the figures of 4 are double that those of 5, etc.
This reasoning can be applied to the series saying that the series of 1 is double that those of 2, the series of 2 are double that those of 3, the series of 3 are double that those of 4, etc.
This ideal distribution is not fulfilled, and we can only assert is that while goes increasing the number of plays, the distribution will be gone approximating every time more to this ideal distribution. It can be that never it is fulfilled exactly, but the difference between the percentage that would correspond to every series taking into account the number of plays and the real will be every time smaller.
The ideal distribution of the series in 247 plays would be this:
SERIES PLAY %
1 series of 7 = 7 plays 0.78
2 series of 6 = 12 plays 1.57
4 series of 5. = 20 “ 3.15
8 series of 4. = 32 “ 6.30
16 series of 3. = 48 “ 12.59
32 series of 2. = 64 “ 25.19
64 series of 1. = 64 “ 50.39
TOTAL 127 series. 247 plays. 100.00
If we go increasing the number of plays the corresponding percentage to the series of 1 goes approximating to 50%, that of the series of 2 to 25%, that of the series of 3 to 12,5%, etc.
VERY NEAR THE INFALLIBLE METHOD.
In the book "THE COMPLETE BOOK OF CASINO GAMES" the authors explain a method used by a Spanish systemist called García. Taking this method, which we will explain below, as a starting point, the authors elaborate their roulette system. We will not go into analysing the efficiency or mathematical base of this last, but we consider its practical application excessively complex. We also take it as a starting point, but to arrive, as we will see later, at quite different results. GARCIA’s system consisted of the following:
If the first play is BLACK, in the following one you bet 1 chip on the break of the series, that is to say, on RED. If the second play is RED you win 1 chip and you restart betting 1 chip on BLACK.
GRAPHIC 2

If the second play has not been RED but BLACK, you bet 3 chips on RED. If the third play is RED you get 2 chips (3 won minus 1 lost in the first play) and you restart betting 1 chip on BLACK.
GRAPHIC 3
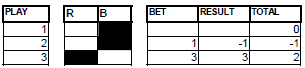
If the third play has been BLACK you bet 7 chips on RED. If the fourth play is RED you get 3 chips (7 won minus 4 lost) and you restart betting 1 chip on BLACK.
GRAPHIC 4
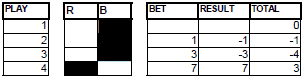
If the fourth play is BLACK, you don’t bet more on the break of the series. We’ve had a series of 4. The system expects a series of 7, that is to say, 3 more BLACK. So far the losses amount to 11 units, divided into 3 bets (4, 4, and 3).
GRAPHIC 5
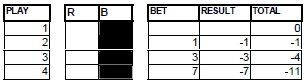
Fifth play: you bet the first 4 units on BLACK. If the fifth play is a BLACK, you bet the following 4 units on BLACK in the sixth play. If you also win then you bet the last 3 units on BLACK in the seventh play. If the game has gone by in this manner you have obtained as net profits all the ones originated by the series of 1, of 2, and of 3 that have appeared until then.
GRAPHIC 6
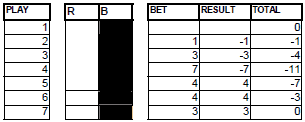
However, when one of the recovery bets of the plays 5, 6, or 7 fails, this loss is added to the one which still has to be recovered and we restart the cycle betting a unit on the intermittence, 3 units on the break of the series of 2 and 7 on the break of the series of 3, until a series of 4 appears again.
GRAPHIC 7
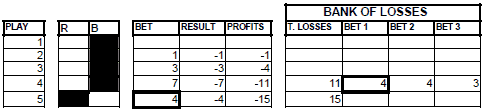
GRAPHIC 8
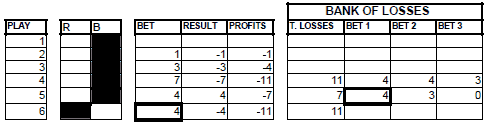
GRAPHIC 9
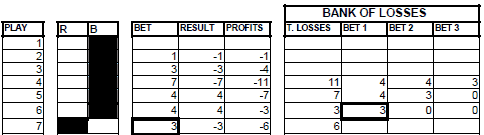
An example, the game goes by with the profits obtained with the series from 1, 2, and 3 until a series of 4 appears. The loss amounts to 11 units. In the following play, you bet 4 chips on the formation of a series of 5 and you lost. These 4 chips are added to the previous 11 which amount to a total of 15. The cycle restarts until a series of 4 appears that will entail another loss of 11 units. This loss will have to be added to the already existing 15, amounting to a total of 26, which will be divided into 3 (9, 9, and 8). In the fifth play, we would bet 9 chips on the continuation of the series.
GRAPHIC 10
As we can see, all the system is based on the appearance of a series of 7 or higher. We know that a series of 7 has a possibility of being formed every 247 plays and we have seen that in a sufficiently large number of plays this prediction is true. But this fact does not occur regularly and in the same way that we can have 3 series of more than 6 in a sequence of 30 plays, we can also find ourselves having to wait for 300 plays until one appears. What are the average losses that you may have to assume waiting for the series of 7?
Working always on the ideal distribution that we know and taking into account that a series of 4 causes that the deficit increases by 11 units more the third part of the already existing one, that a series of 5 does not alter the deficit, and that a series of 6 reduces it 2/3 parts, we have to assume losses of around 330 chips with recovery bets of 110. The deficit is not real since we would have been collecting the profits obtained with the appearance of the series from 1, 2, and 3, and they would be exactly 176 units. To summarise, we would have an effective deficit of 154 chips, and to recover we would have to make bets of 110.
All this supposing that every two series of 4 it appears one of 5, and for every two series of 5, one of 6. What does this system require to put it into practice? Two principal requirements, first to have great capital and second to have nerves of steel to apply it in the game table with real money. But neither of these two requirements would be enough to guarantee the usefulness of the system. The time could arrive, and in fact, we have seen it ourselves several times during the tests we made, where the recovery bets surpassed the maximum bet allowed by the table (540 times the minimal bet). And we have also to take into account the appearance of the zero. This factor is more important the higher the quantities which we can be forced to bet following the system.
2 OBSERVATIONS:
- It is a very risky system that bases all the recovery on a fact that occurs once every 247 plays.
- Setting aside its mathematical possibilities, the system was not making the most of the appearance of the series of 1, 2, and 3. García obtained 1 chip of profit with the series of 1, 2 chips with the series of 2, and 3 chips with the series of 3. But if we apply the progression 3 - 5 - 9, the series of one would produce 3 chips of profit, the series of 2 two, and the series of three 1 chip. The loss caused by a series of 4 would be 17 units instead of 11. The deficit would increase more quickly, but the system is based on recovering all the losses with the first series of 7 or higher. When the series appears, after the usual 247 plays, the profits obtained with Garcia’s system with the series of 1, 2, and 3 are of 176 units and with our progression, they would amount to 272.
GRAPHIC 11

GRAPHIC 12

This is GARCIA’s method. It was necessary to explain it to understand from which starting point we have departed to arrive at the results that, as we will see, do guarantee the success in a percentage near to 100% of the cases and do give us security during the game in comparison to the other class of violent game that guarantees only occasionally this recovery.
To begin with, we will say that if we have to apply a system that bases the recovery of all the losses on a specific fact, we prefer that this fact has more possibilities of appearing than those which had the previous one and that was between 1 and 247.
We pay attention again to the ideal distribution of the series in 247 plays, but now especially in the series of 1. There are 64, but which is their distribution throughout 247 plays? A series does not appear once every 4 plays, and nor do appear the 64 together.
Applying the theory of the figures we can begin to know which would be the ideal distribution of these 64 series.
When a series of 1 appears, there is a 50% possibility that another series of one follows and a 50% possibility that any other series follows (2, 3, 4, 5, etc.).
When two consecutive series of 1 appear, there is a 50% possibility that another series of 1 follows and a 50% possibility that any other series follows.
When three consecutive series of 1 appear, there is a 50% of possibility that another series of 1 appears and a 50% possibility that any other series follows
And so on...
If we apply this on 64 series we obtain an ideal distribution in approximate groups that would remain like this:
- 16 groups of 1 = 16 series.
- 8 groups of 2 = 16 series.
- 4 groups of 3 = 12 series.
- 2 groups of 4 = 8 series.
- 1 group of 5 = 5 series.
TOTAL: 57 series.
We still have 7 series of 1 left to arrive at a total of 64. If we distributed them following the calculation of probabilities, we could have the following distribution:
- 18 groups of 1 = 18 series.
- 9 groups of 2 = 18 series.
- 5 groups of 3 = 15 series.
- 2 groups of 4 = 8 series.
- 1 group of 5 = 5 series.
TOTAL: 64 series.
We have added two to the groups of 1, one to the groups of 2, and another to the groups of 3. What we want to know now is what right of appearance has every one of these groups in the course of 247 plays. This point is easy to verify by dividing the total number of plays by the quantities of appearance of every type of group. These are the results:
- 1 isolated series of 1 can appear every 14 plays.
- 1 group of 2 consecutive series of 1 can appear every 27 plays.
- 1 group of 3 consecutive series of 1 can appear every 49 plays.
- 1 group of 4 consecutive series of 1 can appear every 124 plays.
- 1 group of 5 consecutive series of 1 can appear every 247 plays.
García’s system tried to recover the losses with 3 consecutive bets in the 5th, 6th, and 7th plays of a series of 7. The number of series of a given length is equal to the sum of all those of a higher length. This is the same as saying that the series of 1 is in opposition to all the series of 2, 3, 4, 5, etc. together. We will take advantage of this information that the calculation of probabilities gives us to put it into practice in the following way:
- We will not attempt to obtain direct profits with the series of 1.
- We will bet 1 unit on the break of the series of 2, 3, and 4. Each of these series will report us 1 chip of profit.
- We will not bet to obtain profits on the series of 4 or higher.
- We use the series of 1 to recover the losses produced by the appearance of the series of 3, 4, and 5.
- We will attempt to recover the deficit in 2 bets on a group of 2 consecutive series of 1.
But if a group of 2 is valid, it is also valid one higher than 2. If we add all the groups of 2 and higher there is a total of 17 groups that should be used throughout the game to cancel the deficit and leave as net profits the ones produced by all the series of 2, 3, and 4.
A group of 2 consecutive series of 1 or higher can appear every 15 plays. We have already obtained a great advantage, as we do not have to wait for one chance every 247 plays to cancel the deficit, during the game, we will be able to cancel it on average 17 times. This fact, as we will see in the practical demonstration, makes both the losses and the recovery bets more reasonable in comparison to García’s system and give us more security during the game.
THE MECHANICS OF THE GAME.
- At the beginning of the game and as long as the deficit to recover is 0, we will pass 2 plays of indication.
- We will bet in the 3rd, 4th, and 5th plays on the intermittence.
- Every time a play is won we restart the cycle.
- The lost chips go to a bank of losses and the total figure is divided into 2.
If a series of 2 appears, we will win a chip in the 3rd play.
GRAPHIC 13

If a series of 3 appears, we will win a chip in the 4th play, but we will have lost one in the 3rd play.
GRAPHIC 14

If a series of 4 appears, we will win a chip in the 5th play, and we will have losses of 2 units in the 3rd and 4th plays.
GRAPHIC 15

And if a series of 5 or higher appears, we will have losses of 3 units caused by the 3rd, 4th, and 5th plays.
GRAPHIC 16

- This deficit is divided into 2. When the break of a series occurs, we expect then the appearance of two consecutive series of 1. We have to bet half the deficit on the intermittence. Two things may happen:
- The first bet is won. We discount the bet made from the deficit, and we still have to recover the other half of the deficit. In the following play, we bet the remaining half. If we won, the cycle is completed and we wait again for a series of 2 and bet on the break. We will have won as many units as series of 2, 3, and 4 have appeared up to now.
- The recovery bet is lost (first or second). There has been a series of 2. The loss is added to the deficit and we continue to bet a chip on the break of the series of 2, 3, and 4, keeping the chips won and adding to the bank of losses the ones caused by the series of 3, 4, and 5. When the first intermittence occurs, it will be time to try again the recovery of the deficit in 2 consecutive bets.
GRAPHIC 17

The mechanics of the game may seem complicated. But it will not seem so, once you see them in practice, in a real sequence. At the same time, we will see how the game control sheets have to be.
When the zero appears. we can mark the box in which it has appeared if this interests us for statistical effects; the play will be considered void to the purposes of the game, but we can not assume the loss and put it in the bank of deficit to recover, since this would alter enormously our predictions. The loss caused by zero will be half the bet made, and in the following play, the same bet will be made. Since we can not include this loss with the general ones caused by the series of 3, 4, and 5, we will have to count it subtracting it from the total profits.
GRAPHIC 18
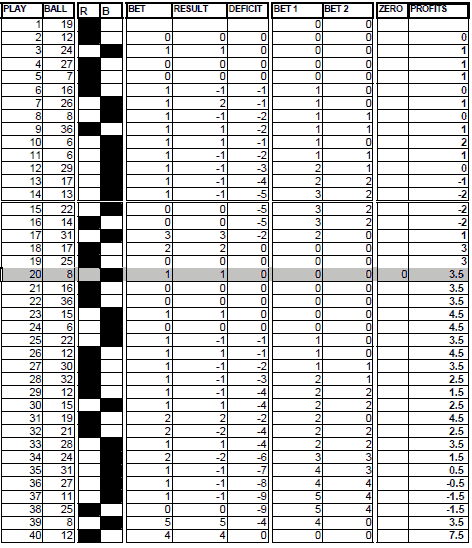
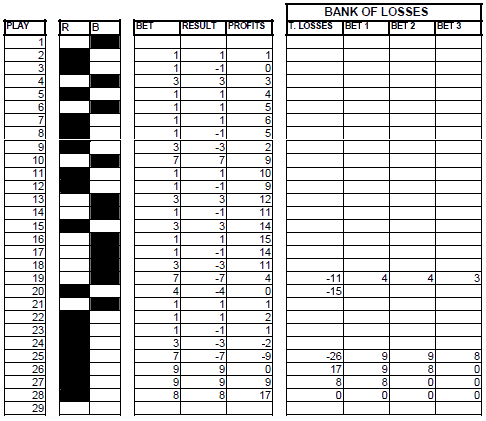
Play number 1: RED.
Play number 2: RED.
Play number 3: 1 chip bet on BLACK. The chip won passes directly to the PROFITSbox (produced by a series of 2).
Play number 4: No bet as there is no deficit to recover.
Play number 5: No bet. We wait for a series of 2.
Play number 6: There has been a series of 2. We bet 1 chip on BLACK. It appears RED. We write the loss in the DEFICIT box, and as it is not possible to divide it into 2, we write a 1 in the box BETS 1 and a 0 in the box BETS 2.
Play number 7: There has been a series of 3. We bet a chip on BLACK. The chip won goes directly to PROFITS. The deficit continues the same.
Play number 8: In the previous play there has been intermittence. We bet the first recovery bet (BET 1) on the intermittence and we lose. The lost chip is added to the previous deficit and is split into 2 recovery bets (1 and 1).
Play number 9: Series of 2. 1 chip is bet on the intermittence and is won. It goes to PROFITS directly.
Play number 10: In the previous play there has been. We make the first recovery bet (1) on the intermittence and we win. We subtract it from the deficit and there is still the second recovery of 1 left.
Play number 11: The second recovery bet fails. We add it to the existing deficit, which becomes again of 2.
Plays 12, 13, and 14: The lost chips are added to the deficit, and every time it is increased, it is divided into 2.
Play 15: In play 14 there has been a series of 5. It does not interest us for the game. We have to wait again until the first intermittence occurs; that will be the sign to reactivate the bets.
Play number 16: No bet, but it is the sign so that, in the following play we make the first recovery bet of the deficit.
Play number 17: Fist recovery bet made and. Still, the second recovery is left.
Play number 18: The second series of 1 that allows us to cancel the deficit. In the PROFITS column, there are reflected the chips won that are equal to the total of series of 2, 3, and 4 that appeared in the sequence.
Play number 19: A new cycle starts with the same mechanics of the game.
Play number 20: Zero. The bet at this time was of 1 unit. We write in the corresponding column and we update PROFITS. In the following play (it would have been 21, but for us, it is 20 again) we make again the bets that the system tells, making the relevant operations.
Plays 21 to 40: Same mechanics of the game. In-play 40 we win the second recovery bet and the deficit is canceled. As net PROFITS we obtain 7.5 units, 8 for the total from the series of 2, 3, and 4 appeared, minus the loss produced by the appearance of the zero in the play 20.
COMMENTARIES:
- We can see in play 37 that the recovery deficit indicates - 9 and in reality, it is - 1.5 units.
- The isolated series of 1 does not alter the deficit and in some phases of the game, they allow us to cancel it (when we have only pending recovery bet).
- The bets are relatively lower in comparison with the GARCIA’s system.
- The yield of the system, as long as you closed all the recoveries, is the sum of all the series of 2, 3, and 4 minus the losses produced by the zeroes (approximately one chip every 5 plays).
So far the theory has been explained. What the reader and potential player is interested in knowing is which practical possibilities has the system.
Now we will present a very critical situation (extracted from a real game) so that the reader can be conscious of what, apart from the yield and advantages of the system, he should be prepared to face if he wants to apply the system without limiting at no time the recovery progression.
GRAPHIC 19

GRAPHIC 20
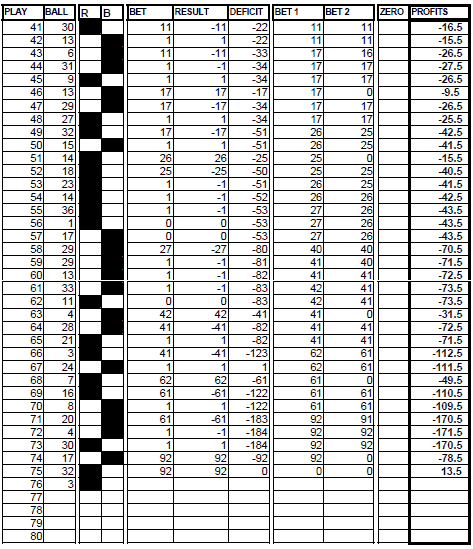
COMMENTARY OF THE SEQUENCE:
- In-play number 1 we had closed the previous recovery.
- Long series have prevailed. They have the advantage that they make the deficit increase more slowly, but the yield, when the recovery is achieved, is inferior.
- When short series appear the theoretical deficit is doubled more quickly, but you get direct profits, and there are also more possibilities of the appearance of individual groups and closing of the recoveries.
- We have nearly reached the limit. We still could have found 2 failed bets in the first recovery without surpassing the limit.
It is an extraordinary situation, as the interval of 15 plays has been multiplied by 5 in plays in which, theoretically, 2 consecutive series of 1 should appear. Can there be a greater interval? Yes, of course, there is no mathematical rule that prevents it, though one must admit that the possibilities of appearance are minimal.
The possibilities of success increase as the initial capital increases. On the other hand, the yield of the system has some clear limitations and depends on 2 factors:
- Several series of 2, 3, and 4 appeared during the game. We have already seen that when prevailing the long series, the deficit increases more slowly and the yield is smaller, and vice versa, when short series appears the recovery interval will be shorter, but the yield higher.
- Losses caused by the zero.
The average yield of the system oscillates between 0.20 and 0.25 chips by play.
If we revise all the methods and bet systems knows, none can guarantee with such a low risk such a high percentage of success. The reader who is interested in the topic can compare, in the book mentioned at the beginning of the chapter, the results to which the authors arrive starting from the same method (García), with those which obtains our system. It is extremely complex to put it into practice, the authors speak of a necessary capital of hundreds of chips and the yield that their system obtains is of a chip every 20 plays (0.05 chips by play).
The sequence presented in these pages is prejudicial to our system. Nobody should make the easy mistake of applying any other system and seeing that it is successful, think that it has found the definitive solution to the problem. We have to remember that every system has a favorable situation and an unfavorable one and that we simply have to try and face the bad one enduring without arriving at the limit, to take advantage and recover when the situation is good.
VARIATIONS OF THIS SYSTEM.
There can be many variations and as always the possible profits are in direct relationship to the risk that one wants to take.
With the same risk, same yield, and the same percentages of success there are the following options:
- Attempt the recovery in three bets on the groups of 3 consecutive series of 1 and higher. Every group should appear every 30 plays. The deficit rises more slowly as we are dividing it into 3 and the groups of 2 allow us to reduce it in a third party.
- In a group of 4 consecutive series of 1. There are three groups in total and the appearance interval is of one every 82 plays. The groups of 2 reduce the fourth part the deficit to recover, and those of 3 reduce it to half.
- In those of 5 we would be waiting for a phenomenon that has a possibility of occurring every 247 plays, and though the deficit rises very slowly and the inferior groups (2, 3, and 4) produce a certain relief, we consider that we would be playing too much time under the pressure of recovery. And we have seen in the case of the group of 2 that the appearance of the phenomenon (though it is an extraordinary situation), can multiply by five the average interval of appearance.
With a greater risk of capital there can be many options:
- Bet on the break of the series of 1. When attempting the recoveries we have to add a unit every time, and the yield increases in a way proportional to the risk of not being able to assume the recovery deficit. In this case, the yield can oscillate between 0.30 and 0.40 chips per play.
- Lengthen the bet on the series higher than 4.
- Intensify the bets in the first series (e.g.: 3 units in the series of 1, 2 units in the series of 2, and 1 unit in the remaining series).
The reader will probably need the graphic representation of the possibilities of the system, but we will not make it, and we will now explain the cause:
We are very satisfied with the results, obtained from a method which is of difficult practical application, but yet, these results can be improved.
Can we play in a way yet more intelligent? Of course, we can do it and we can manage to minimize the scarce possibilities that chance has of leaving victorious, but, furthermore, we will have an almost total tranquillity during the game. Our method will come closest to what it could be called the "infallible" method, and the possibilities of success will be 98%. We will now explain this:
The previous method puts all the losses produced by the series of 2, 3, and 4 in the same bank and attempts to recover them in 2 bets on 2 consecutive series of 1. We have a total of 17 groups of series of 1 that have to recover the deficit caused by the sum of all the series of 2 or higher, which makes in total 31. If we add to this figure all the series of 2 and higher that prevent us from recovering (63), this means that we are fighting at a clear disadvantage against the BANK. In short sequences with only the appearance of series higher than 1, we can find that the deficit increases very quickly and exceeds our initial limit. And just after exceeding ourselves, groups of series of 1 appear that are no longer used to us. We have to establish a more egalitarian relationship with the BANK.
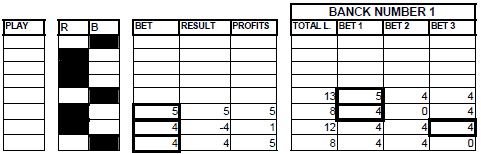
We achieve this by dividing this deficit into three independent banks (everyone will make his recovery). We explain the procedure below:
We will bet a unit on the break of the series of 2, 3, and 4. The obtained units are direct profits.
The units lost when appearing a series of 3 will be put in a bank of losses number 1, and they will be divided into 3. For the chips of columns 1 and 2, we will attempt to recover them in 2 consecutive bets with the appearance of a group of 2 consecutive series of 1 or higher.
GRAPHIC 21

When they appear 2 series of 1 consecutive, in the following play is not bet the figure of the column number 3. The figure of column number 3 will be bet only in the third play to the break of the series of 2 (32 series).
When it is lost one of the recovery bets (1, 2, or 3) is added to the deficit and this is returned to divide between 3.
GRAPHIC 22
Possible causes:
GRAPHIC 23

GRAPHIC 24

GRAPHIC 25

GRAPHIC 26

GRAPHIC 27

GRAPHIC 28
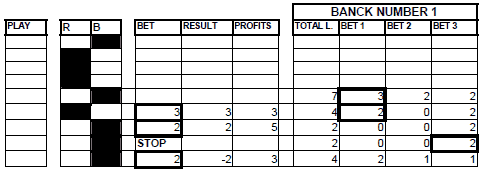
The units lost when appearing a series of 4 will be put in a bank of losses number 2, they will be divided into 2, and we will attempt to recover them in 2 consecutive bets with the appearance of a series of 3: when a series of 2 appears, we will play on the appearance of a series of 3 and we will make the first bet on the continuation of the series and the following on the break.
GRAPHIC 29
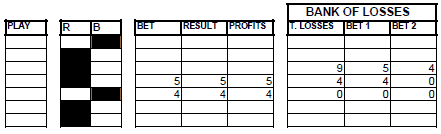
The units lost when appearing a series of 5 will be put in a bank of losses number 3, they will be divided into 2, and we will attempt to recover them in 2 consecutive bets with the appearance of a series of 4: when a series of 3 appears, we will play on the appearance of a series of 4 and we will make the first bet on the continuation of the series and the following on the break.
GRAPHIC 30
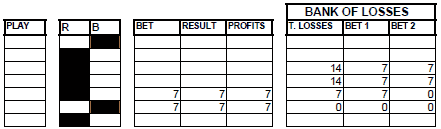
Every bank of losses is independent of the other and has as objective to close its recovery. We recover the losses produced by a series with the appearance of an immediately inferior one in the cases of the series of 4 and 5, and in the case of those of 3 we continue to make it with the groups of 2 consecutive series of 1 and 32 series of 2
1) RECOVERY WITH THE GROUPS OF SERIES OF 1 AND SERIES OF 2
(BANK OF LOSSES NUMBER 1).
With 49 valid groups, we attempt to recover the losses produced by sixteen series of 3, two of 6, one of 7, and the ones produced by the 31 series higher to 2 when failing the first recovery bet (increases in 1/2 the deficit).
2) RECOVERY WITH THE SERIES OF 3 (BANK NUMBER 2).
With 16 groups we attempt to recover the losses produced by eight series of 4, two of 6, one of 7, and the ones produced by the thirty-two series of 2 when failing the first recovery bet (increases in 1/2 the deficit).
3) RECOVERY WITH THE SERIES OF 4 (BANK NUMBER 3).
With 8 valid groups, we attempt to recover the losses produced by four series of 5, two of 6, one of 7, and the ones produced by the sixteen series of 3 when failing the first recovery bet (increases in 1/2 the deficit).
We have improved a lot but as it is not still enough since we have a recovery bank (number 1) which gives too many facilities to the BANK and in a critical situation it would take us beyond our initial limit. We know also, thanks to the analysis of thousands of plays that, when a given phenomenon does not want to appear, little can traditional methods do. We will put an example: we can have 0 in the bank's number 1 and 3 and an average deficit in the number 2. So we would only need a series of 3 to cancel it (a series of 3 should appear regularly once every 15 plays, but we have already seen that this theoretical interval can be multiplied by 5 in practice). In these moments, during 50 plays, we see the appearance of a sequence (that it may be only once in 1000 plays, but when it happens makes our method useless), with many series of 1 and 2 chained with series of 4 and higher that make the deficit of bank number 2 quickly exceed our limit. Our predictions based on the calculation of probabilities will be of no use.
How to solve the problem? The solution is given to us by chance itself: when a given phenomenon does not appear, it means that others are appearing. When a series of 3 does not appear, others must appear (1, 2, 4, 5, etc.). This is the key to the problem, to avoid that the absence of a given phenomenon should be solved with this same phenomenon. If we can make the absence of a given phenomenon be solved, at least in part, by 2 different ones, we will avoid in 98% of occasions the collapse of the system.
We do not like using the term 100%, since we know that a situation that has not appeared in 10000 plays can present itself in the least unexpected moment, but, when we finish explaining the system, all the readers will have to agree with us that this is the method that comes closest to the term "infallible" if it can not be called this way.
What is certain is that you will be prepared to endure critical situations that no other method could resist, finally recovering all the losses and obtaining a yield more than acceptable. To all this, we have to add the fact that the investment of capital that we need to put into practice is really low.
How can we make the absence of a phenomenon be solved by the appearance of others opposed? When a recovery bet fails and it is equal to or higher than 3 units, instead of adding it completely to our bank, it will be distributed into 3 banks.
Ex: We have in bank number 2 a deficit of 9 units ( there appear series of 2, of 4 and higher and none of 3). The first recovery of 5 fails. Instead of adding it totally to bank number 2 which would make a total of - 14, we divide it into 3 (2, 2, and 1). We add the first 2 units to the previous 9 getting a total of 11, the 2 following units are added to bank number 1 and the remaining unit is bank number 3. We are avoiding that the absence of series of 3 increases the deficit in bank number 2 and at the same time we may obtain a series of 4 or 2 series of 1 consecutive that make us reduce the deficit in one or two thirds.
IMPORTANT: The division between the 3 banks only will be affected when it will be the first recovery bet (column 1 of the banks 1, 2, and 3) and when we affect the only one recovery of column 3 of bank number 1. Motive: When it is tried to the second recovery, it will not alter the original deficit of this bank and there has not of altering the deficit of the other banks.
GRAPHIC 31

GRAPHIC 32
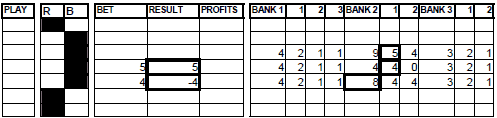
A very important detail, when the failed recovery bet is divided into 3, the first part is added to the corresponding bank, and the following two are added to the remaining banks from left to right. This rule has an only exception when the deficit surpasses 15 units.
As a precaution against the persistence of the situation, we will add to this bank the smaller part and the remaining two will be put in the same way from left to right in the remaining banks.
GRAPHIC 33
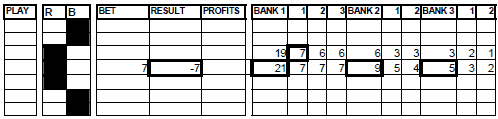
In the case of 2 banks exceeding 15 units, we will follow the priority from left to right and the remaining quantity will be put in the last. And in the totally unlikely fact that 3 banks exceeded 15 units, we will follow the initial procedure.
GRAPHIC 34
We have of taking advantage also the greater appearance of the one phenomenon and the closes to zero or important decrease of the deficit of the corresponding bank, to get lighter the deficit of the other 2 banks. We establish a maximum deficit and closing figure for every one of the banks:
DEFICIT CLOSING
BANK NUMBER 1: 15 5
BANK NUMBER 2: 10 4
BANK NUMBER 3: 6 0
When one of the banks closes, if the other banks even or surpass the indicated figure, their deficit will be divided with the bank that there has closed. We will put 3 examples:
BANK NUMBER 1 remains with an inferior deficit of 5 units. The bank number 2 super 10 units. Bank number 2 divides its deficit with bank number 1.
DÉFICITS BEFORE DEFICITS AFTER
BANK NUMBER 1: 3 8
BANK NUMBER 2: 13 8
BANK NUMBER 3: 4 4
BANK NUMBER 2 remains with an inferior deficit of 4 units. The bank's numbers 1 and 3 divide their deficit with bank number 2.
DEFICITS BEFORE DEFICITS AFTER
BANK NUMBER 1: 17 11
BANK NUMBER 2: 3 10
BANK NUMBER 3: 12 11
BANK NUMBER 3 closes to 0. Bank number 2 divides his déficit with bank number 3
DEFICITS BEFORE DEFICITS AFTER
BANK NUMBER 1: 6 6
BANK NUMBER 2: 17 9
BANK NUMBER 3: 0 8
GRAPHIC 35

The balance between the different deficits is important so that the bets are not increased quickly when one of the phenomena delays his appearance. For so much, always exist the conditions of the values of LIMIT and CLOSE we can to do the operations explained previously.
We will play as there were 3 different players, but mutually helping them in critical situations. The first player attempts to obtain as net profits the chips produced by the series of 2, the second player makes the same with the series of three, and the third player with the series of 4.
After an intermittence, in the second play, we will play a first recovery bet of bank number 1.
GRAPHIC 36

GRAPHIC 37

GRAPHIC 38

When we have a series of 2, in the third play we will make 2 bets, 1 chip on the
break of the series, and only recovery bet of the column number 3 of the bank 1, and
at the same time a first recovery bet of bank number 2.
GRAPHIC 39

When a series of 3 appears, in the fourth play we will make 3 different bets, 1 chip on the intermittence, a second recovery bet of bank number 2, and the first recovery bet of bank number 3.
GRAPHIC 40

When a series of 4 appears, in the fifth play we will make 2 bets, 1 chip on the intermittence and the second recovery bet of bank number 3.
GRAPHIC 41

As we can see, in 3 plays we will make opposed bets but we have to see the procedure followed by each bank as an independent process that has an only purpose: to obtain, on the one hand, greater resistance against adverse situations and besides net profits consisting in the sum of all the units bet on the break of the series of 2, of 3 and 4.
GRAPHIC 42

The real bet will be the result of adding or subtracting the different bets. It is easy to understand that, unlike the previous method, in this, we will normally have some recoveries still to be closed, but it is also possible to close them all with a given sequence (series in diminishing order: 4 - 3- 1 - 1 or other sequences that would leave us a minimal deficit in some of the banks). The most remarkable fact is the calmness that it gives us during the game and the great resistance that is obtained by having the deficit divided into 3 and being able to ease the bank that causes us more problems.
The only defect of the system is its relative complexity as we have to make so many operations in the same play, but this complexity reduces with practice. For all systems it is advisable to make many tests before playing with real money, in this, we emphasize the importance of assimilating well the mechanism so that you make all the operations automatically and you can perfectly control the game.
The last point: Appearance of the zero. Until the moment we thought it unnecessary to risk to recover the losses produced by its appearance, but after all the tests made and relying on the greater resistance that has the method, we will let it to the election of the player.
The procedure to follow when it appeared would be to divide the losses into 3 and add them to the banks, but from right to left, because of the reason previously explained (ex: BET: 8. LOSS: 4. ORDER: 1, 1, 2).
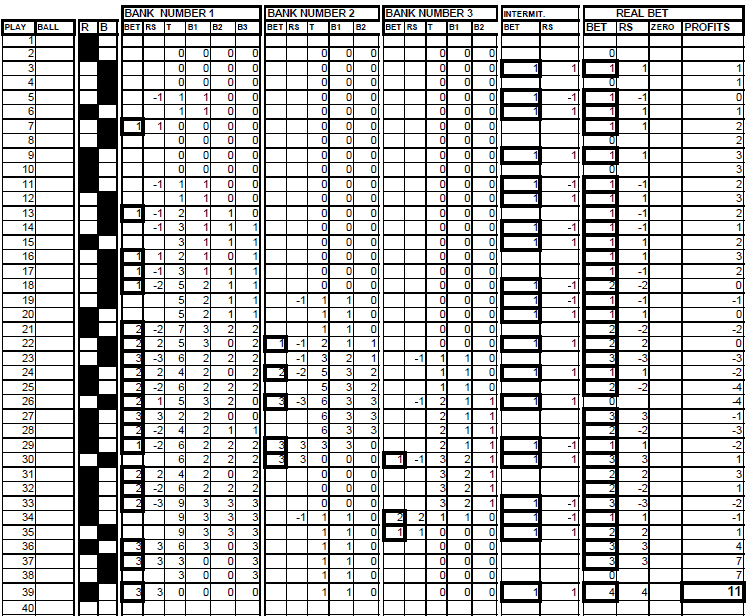
We will work on the sequence of the graphics 19 and 20, a very critical sequence so that the results can be compared and demonstrate the theory explained so far.
GRAPHIC 43

GRAPHIC 44

COMMENTARY ON THE SEQUENCE:
PLAYS 3, 4, and 5: We bet a chip on the intermittence and the losses go to the respective banks. As there is no previous deficit, we make only one bet.
PLAYS 6, 7, and 8: No bet. We wait for the first intermittence, which happens in play number 8.
PLAY 9: We make the first recovery bet of bank number 1. It has previously appeared a zero. We repeat the bet, we added a unit to bank number 1, and we reflect the loss in the PROFITS column.
PLAY 10: We have a series of 2. First recovery of column 3 of bank number 1. We also make the first recovery bet of bank number 2 on a series of 3 and we bet a unit on the intermittence. In this case, the real bet is 1.
PLAYS 11 and 12: Recovery in bank number 1
PLAY 13: Pay attention that the chip lost when playing on the intermittence is added to bank number 1.
PLAY 14: We have a series of 3. We make a second recovery of bank number 2, the first recovery of bank number 3 and we bet a chip on the intermittence. The real bet is the result of adding the chips bet on the intermittence and the break of the series of 3 (bank number 2) minus the bet made on the continuation of the series (bank number 3).
PLAY 16: We affect the recovery bet of column 3 of bank number 1.
PLAY 17: We make the first recovery bet of bank number 3 and we bet a chip on the intermittence. This lost chip goes to bank number 2.
PLAY 18: We make the second recovery bet of bank number 3 and we bet a chip on the intermittence. The real bet is the sum of these two bets.
PLAY 20: We lose the second recovery bet of bank number 1.
PLAY 26: It has been lost the second recovery bet of bank number 1 and it is equal to 3 units. It is not distributed between 3 banks.
PLAY 29: It has been lost the first recovery bet of bank number 1 and it is equal to 4 units. It is distributed between 3 banks.
PLAY 45: Bank 3 is super the limit, bank 2 is under the value of close. The deficits are added and distributed. The same fact occurs in plays 51 and 53.
PLAY 55: We have made a second recovery bet and it has failed. But we have also lost the chip bet on the intermittence. Observe that the result is -3 and the deficit in this bank goes from 2 to 5 units.
PLAY 73: We have closed the recovery in bank number 2 and we have a deficit higher on 10 units (- 20) in bank number 3. We divide it with bank number 2 so that the two banks have a deficit of 10 units. Bank number 1 continues unalterable.
PLAY 78: We affect a first recovery in the bank number. 3 and is winner At the same time the chip bet to the intermittence and lost is added to the bank number 2.
PLAY 79: We affect the second recovery in bank number 3 and are the winner. None of the banks 1 and 2 super theirs limits and continue inalterable.
We end the sequence with a deficit of - 2 chips. We still have to recover 9 units of bank number 1 and 9 of bank number 2. It would make a total of 16 chips that are the 16 series of 2, 3, and 4 appeared.
This is a very unfavorable sequence for the system (with a clear dominance of the large series on the shorts) and no matter what it ends with losses. What imports it is to know how resisting it when is presented, for to can win after with the "normal" sequences. Everybody knows to win in favorable situations, but well few know to make it unfavorable. At any rate, we will present a short sequence of 40 spins more current in the game table and we will see clearly which is the yield that can obtain the system with alternated gambling (graphic 45).
COMPARISON WITH GRAPHICS 19 And 20:
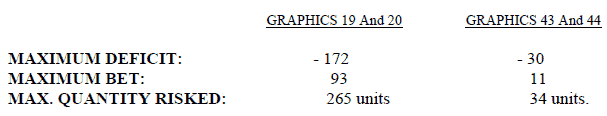
GRAPHIC 45
GENERAL COMMENTS ON THE METHOD:
- In alternation situations of all the series, it will go on closing the different recoveries and obtaining profits.
- In critical situations, it avoids the collapse by preventing the rapid increase of problematic deficits by dividing the highest bets into the three banks and making that always one of them closes the recovery.
- The maximum risked quantity has been 34 units. Normally we would begin the game with 50 units, therefore, we would be yet far from the limit.
- This sequence can appear but rarely. Normally, the game is very changing (with alternation of all kinds of series) what has always made it very difficult to apply an effective method for all kinds of situations. And one must recall that at the end of 250 plays, the distribution of the series will have come closer to the one which we know as ideal. Logically, after this sequence, there will come another difference that will take us back to void deficits or non-existent and the profits will be put on the same level with the total of similar series of 2, 3, and 4.
- We achieve a great resistance to overcome the most adverse situations.
- The necessary initial capital is low. With 50 chips we cover sufficiently any critical situation.
- The method gives great confidence because we know that sooner or later we will lose some of the banks and if there is some indeed problematic one, we will be able to ease it.
- Our position is much more comfortable. Unlike before we do not have to rely on the appearance of an only phenomenon to close the recovery. When this did not happen or took much time it appears, we could ourselves be compelled to abandon the game having lost all the initial capital. Now we have 3 different options and each one collaborates with the others.
- The losses caused by zero can be recovered. A possible option is to wait until they add up to 3 units and to distribute them into 3 banks. There are other options, but we leave them to the player’s imagination. The only thing will be to add a column next to zero, in which we control the total of these losses.
PLAYS IN THOSE WHICH THE REAL BET IS ZERO:
ONLINE live CASINO: We must of betting. We will play always a unit to the break of the series. The chips wined go directly to profits. The lost chips will be put on bank 1 or 2 (the one which has a smaller deficit), never in bank 3.
Depending on the class of game, at the end of the session of 250 spins, it can suppose some profits of 40 chips more, but the risk is greater.
REAL ACTION: I advise not to bet since the possibilities of success of the system will be greater.
In any case, the player can choose between not to bet (and take advantage to be relaxed) or following the previous procedure.
THE THREE KEY FACTORS OF THE SUCCESS OF THE METHOD:
- RECOVERY OF LOSSES BETWEEN 3 INDEPENDENT BANKS
- DIVISION OF THE LOSSES SUPERIOR TO 3 UNITS BETWEEN 3 BANKS.
- A DECREASE IN THE DEFICITS IS MORE PROBLEMATIC WHEN A BANK CLOSES TO ZERO OR REMAINS WITH A DEFICIT VERY LOW.
YIELD OF THE SYSTEM IN 250 PLAYS.
- Not recovering the losses caused by the zero: 50 - 60 chips.
- Recovering the losses caused by the zero: 55 - 65 chips.
AVERAGE YIELD OF THE SYSTEM: Between 0.20 and 0.30 chips per play.
In this method, we can speak of a team game but with only one player. The only defect it has (the advantages we have already seen) is the great concentration that demands on the player at all times, and the fact of having to make until four different operations.
Is there any form of simplifying the system? Yes, and we present it below:
The situation is complicated much when the deficits of the banks are very high.
Then it is very difficult to control the nerves (we are losing) and to accomplish all the necessary operations in each spin. There is a way yet simpler and intelligent of play, to divide the session in games shorter using the following parameters:
PROFITS TO OBTAIN: +5 +10
INITIAL CAPITAL: 5 +10
We will stop the game and we will return to begin it with the banks to ZERO when:
- Profits + following bet >= PROFITS TO OBTAIN (The profits obtained until the moment, plus the bet that we would have of effecting to the following play surpass 5 or 10 units).
- Risky capital + following bet >= INITIAL CAPITAL (The losses plus the bet that we would affect in the following play surpass 5 or 10 units).
These conditions will be performed every 20 - 60 spins. In a session of 250, we will play an average of 4 - 8 games. The final balance will be favorable, at all times we will control the possible losses and we will be able to stop the game when we want.
TOTAL CAPITAL: 25 - 50 chips (necessary to confront the total of 250 spins).
Playing in this way we obtained:
- To avoid the nerves since NEVER we will have of confronting large recoveries.
- The operations between banks will be minimal and will be able to do them with much easiness.
- The bets will be ALWAYS small.
- When we add the loss produced by the zero to the deficits it will not alter them too.
- We will abandon the game if the total Profits arrive at a given figure (example: +20 - +40).
Test the program (two options) with these parameters and you will see how always at the end of 250 spins the balance is favorable.
Playing in this way the game is simplified much. In any case, we believe that is worth the trouble to make many tests until perfectly assimilating the mechanism, obtaining the necessary agility. Roulette players know that a method that guarantees such a high percentage of success in ALL situations could not have a relatively easy application.
If someone believes that its application is too complex, he always has simpler options previously explained in these pages, but they will not guarantee the same results. We limit ourselves to explain how to play in the most intelligent possible way and we wanted to demonstrate that the set phrase heard so many times since this game was invented - THE BANK ALWAYS WINS - is not true.
Try This Strategy in TOP Live Casinos
Dont forget: This strategy collected from internet. LiveCasinoGuru is not responsible for the accuracy of this information. It is presented for information purposes only. Our task is to collect and present strategies to share experiences. Any possible wins and losses are the responsibility of the player.




